Mathematics OBJ:

1CDAAEABAEC
11AEDDCDCDCC
21CEBDEDCBBC
31CBEEECBDCC
41DBCBCDDBCA
51BCBDCDCCEC

ALWAYS SUBSCRIBE IF YOU WANT YOUR ANSWERS BEFORE THE EXAM

1a)
Log 10(20*-10)-log10(*+3)=log105
(20*-10/*+3)=log10 =5
20*-10/*+3=5
5(*+3)=20*-10
5*+15=20*-10
15+10=20*-5*
25=15*
*=25/15
*=5/3=1 2/3
1b)
Discount percent =15%
Discount amount =#600
Actual amount paid on the article =?
Original amount on the article =*
15%*=#600
15/100* =600
15*=600*100
15*=60000
*=60000/15
*=#4,000
Therefore actual amount paid on the article
=#4,000-#600
=#3,400
Actual amount paid on the article =#3,400

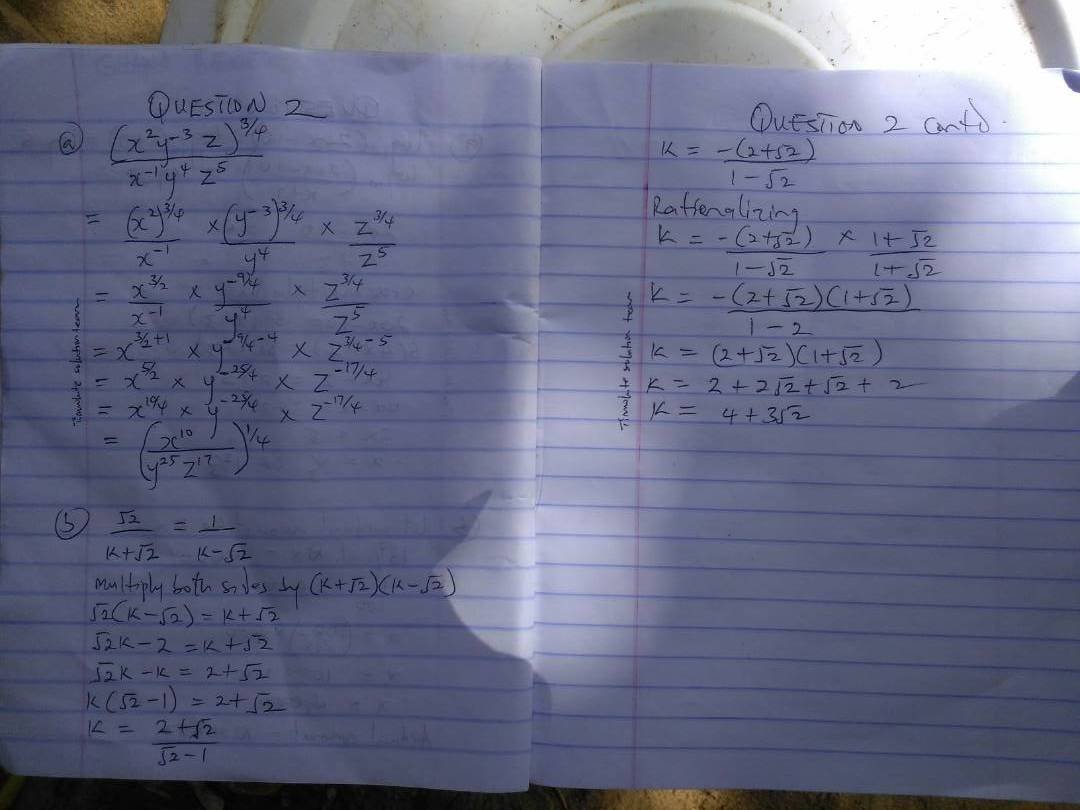
2a)
(X^2 Y^-3 Z)^3/4/X^-1 Y^4 Z^5
= (X^2)^3/4/X^-1 * (Y^-3)^3/4/Y^4 * Z^3/4/Z^5
= X^3/2/X^-1 * Y^-9/4/Y^4 * Z^3/4/Z^5
=X^3/2+1 * Y^-9/4-4 * Z^3/4-5
=X^5/2 * Y^-25/4 * Z^-17/4
=X^10/4 * Y^-25/4 * Z^-17/4
=(X^10/Y^25 Z^17)^1/4
2b)
√2/k + √2 = 1/k – √2
Multiply both sides by (k+√2)(k-√2)
√2(k-√2) = k+√2
√2k-√2 = k+√2
√2k-k = 2+√2
K(√2 -1) = 2+√2
K = 2+√2/√2-1
K = -(2+√2)/1-√2
Rationalizing
K = -(2+√2) * 1+√2/1-√2
K = -(2+√2)(1+√2)/1 – 2
K = (2+√2)(1+√2)
K = 2+2√2 + √2+2
K = 4+3√2

3)
V = Mg√1 – r²
Square both sides
V² = m²g²(1-r²)
V²/m²g² = 1-r²
r² = 1 – v²/m²g²
r = √1-(v/mg)²
If v = 15, m = 20, and g = 10
r = √1 – (15/20*10)²
r = √1 – (0.075)²
r= √(1.075)(0.925)
r = √0.994375
r = 0.9972

4i)
length of Arc of the sector
Titter= 72degree, r = 14cm
L= titter / 360 x 2 pie r
==> L= 72/360 x 2 x 22/7 x 14
=44352/2520
=17.6cm
4ii) perimeter of the sector
Perimeter = titter/360 x 2 pie r + 2r
=17.6 +(2×14)
=17.6+28
=45.6cm
4iii) Area of the sector
Area = Titter/360 x pie r^2
=72/360 x 22/7 x (14)^2
=72 x 22 x 196/2520
Area= 310464/2520
=123.2cm^2kg

5a)
Mode = mass with highest frequency = 35kg
Median is the 18th mass
= 40kg.
5b)
In a tabular form
Under Masses(x kg)
30,35,40,45,50,55
Under frequency(f)
5,9,7,6,4,4
Ef = 35
Under X-A
-10, -5, 0, 5, 10, 15
Under F(X-A)
-50, -45, 0, 30, 40, 60
Ef(X – A) = 35
Mean = A + (Ef(X – A)/Ef)
= 40 + 35/35
= 40 + 1
= 41kg

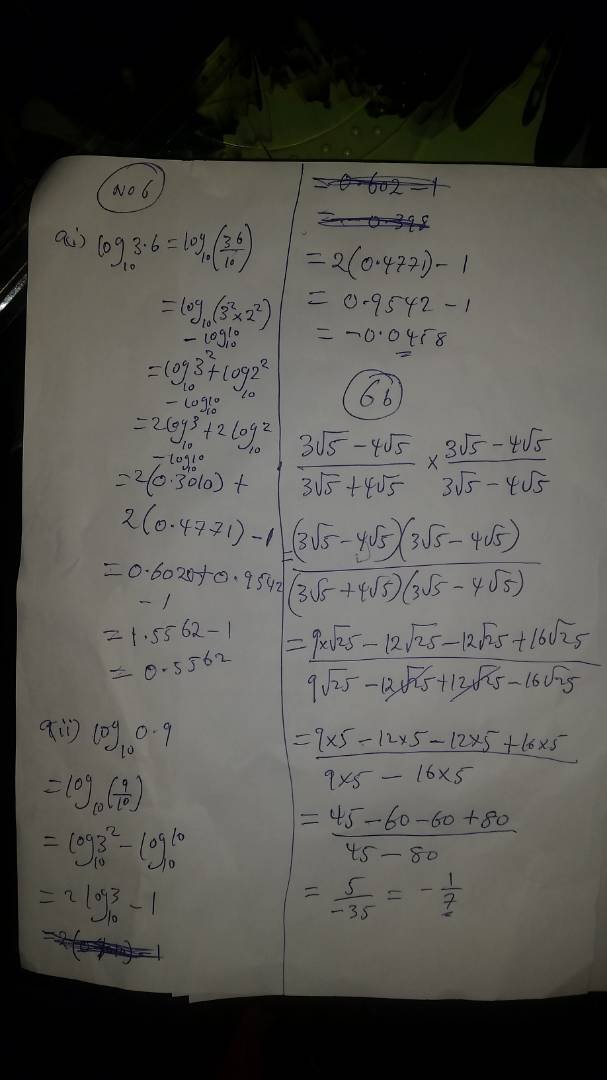
6a)
log2 = 0.3010
Log3 base 10 = 0.4771
(i) Log10 3.6 = Log10 36/10
= log10 36 – log10 base 10
= log10 (9×4) -1
=log10 9+log10 4 – 1
=log10 3² + log10 2² – 1
=2log10 3 + 2log10 2 – 1
= 2(0.4771) +2(0.3010) -1
= 0.9542 + 0.6020 – 1
= 0.5562
6aii)
Log10 0.9
= log10 9/10 = log10 9-log10 10
= 2log10 3 – 1
= 2(0.4771)-1
= -0.0458
= 1.9542
6b)
(3√5 – 4√5)(3√5-4√5)/(3√5+4√5)(3√5-4√5)
= 45 – 60 + 80 = 60
45-60+60-80
= 5/35 = 1/7

7ai)
T3=>a+2d=6(eqi)
T7=>a+6d=30(eqii)
Eqii minus eqi gives
6d-2d=30-6
4d=24
d=24/4
d=6
Common difference=6
7aii)
Putting d=6 into eqi
a+2(6)=6
a+12=6
a=6-12
a=-6
(7aiii)
10th term T10=a+9d
=-6+9(6)
=-6+54
=48
7bi)
T3=>ar²=9/2(eqi)
T6=>ar^5=243/16(eqii)
Dividing eqii by eqi
ar^5/ar²=243/16 divided by 9/2
r³=243/16*2/9
r³=27/8
r³=3³/2³
r=3/2
Putting this into eqi
a(3/2)²=9/2
a(9/4)=9/2
a=9/2*4/9
a=4/2=2
7bii)
Common ratio r=3/2 as above

8)
x=a+by(eqi)
when y=5 and x=19
19=a+5b(eqii)
when y=10 and x=34
34=a+10b(eqiii)
solving eqii and eqiii
a+10b=34
a+5b=19
=>5b=15
b=15/5=3
putting b=3 in eqii
19=a+5(3)
19=a+15
a=19-15
a=4
8i)
Putting a=4 and b=3 in eqi
x=4+3y
This is the relationship between xand y
8ii)
When y=7
x=4+3(7)
x=4+21
x=25
8b)
3x/x+2 – 5x/3x – 1 + 1/3
Find the L. C. M
3(3x-1)(3x)-3(x+2)(5x)+(x+2)(3x-1)/(x+2)(3x-1)(3)
27x²-9x-15x²-30x+3x²-x+6x-2/3(x+2)(3x-1)
Collect like terms
15x²-34x-2/3(x+2)(3x-1)

10a)

Obtuse 105 + reflex Reflex = 255 °
Now 2 w = reflex 2 w = 255 °
W = 255 / 2 = 127 . 5 °
Also 2 x = obtuse 2 x = 105 °
X = 105 / 2 = 52. 5 °
Now EDF = y ( base angles of an isosceles triangle )
BED = X = 52. 5 ° ( angles in the same segment )
EFD + EDF = BED ( sum of interior angles of a triangle equal exterior angle )
Y+ y = 52. 5 °
2 y = 52. 5 °
Y = 52. 5 ° / 2
= 26. 25°
10b )
Draw the diagram
Opp/ adj = TanR
| TB | / | BR | = TanR
100 / | BR | = Tan60°
| BR | = 100 / tan 60
| BR | = 100 √3
| BR | = 100 √3 * √3 / √3
= 100 √3 / 3 m OR 57. 7 m

11a)
x+y/2 =11
x+y= 11*2
x+y= 22 —(1)
x-y= 4 —-(11)
x+y = 22—-(1)
–
x-y= 4—-(11)
____
2y = 18
y= 18/2
y=9
Substitute y=9 in equ 1
x+9=22
x=22-9
x=13
x=13, y=9
x+y= 13+9= 22
Sum of the two number

11b)
(6x + 3) dx
(6x + 3)dx
(6x +3)^6 – (6x + 3)^1
(6 x + 3)^5
(7776x^5 + 243)
38,880x/6 + 243
6480 x^6 + 243x
9(720x^6 + 27x)
11c)
y = x² + 5x – 3 (x = 2)
y = 2² + 5(2) – 3
y = 4 + 10 – 3
y = 14 – 3
y = 11

Gradient of the curve = 11

12a)
Pr of Abu to pass = 3/7
Pr of Abu to fail = 1 – 3/7 = 7-3/7 = 4/7
Pr of kuranku to pass = 5/9
Pr of kuranku to fail = 1 – 5/9 = 9 – 5/9 = 4/9
Pr of musa to pass = 12/13
Pr of musa to fail = 1 – 12/13 = 13 – 12/13 = 1/13
Pr of only one of them passing is
=(3/7*4/9*1/13)+(5/9*4/7*1/13)+(12/13*4/7*4/
=12/819+ 20/819 + 192/819
=12+20+192/819 = 224/819
= 32/117
12b)
10Red + 8green + 7blue = 25
12bi)
pr of different colour is
Prof(RG)+(RB)+(GB)+(BG)+(BR) +(GR)
=(10/25*8/24)+(10/25*7/24)+(8/25*7/24)+(7/25*
=80/100 + 70/600 + 56/600 + 56/600 + 70/600 + 80/600
= 80+70+56+56+70+80/600
= 412/800 = 103/200
12bii)
pr of atleast one must be
=Pr[RB+BR+GB+BG+BB]
= (10/25*7/24)+(7/25*10/24)+(8/25*7/24)+ (7/25*8/24) + (7/25*7/24)
=70/600+70/600+56/600+56/600+49/600
=70+70+56+56+49
/600
=301/600